Propiedades
- El determinante de una matriz es un invariante algebraico, lo cual implica que dada una aplicación lineal todas las matrices que la represente tendrán el mismo determinante. Eso permite definir el valor del determinante no sólo para matrices sino también para aplicaciones lineales.
- El determinante de una matriz y el de su traspuesta coinciden:

- Una aplicación lineal entre espacios vectoriales es invertible si y sólo si su determinante no es nulo. Por lo tanto, una matriz con coeficientes en un cuerpo es invertible si y sólo si su determinante es no nulo.
Determinante del producto
- Una propiedad fundamental del determinante es su comportamiento multiplicativo frente al producto de matrices:
Esta propiedad es más trascendente de lo que parece y es muy útil en el cálculo de determinantes. En efecto, supongamos que queremos calcular el determinante de la matriz  y que
y que 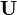 es cualquier matriz con derminante uno (el elemento neutro respecto al producto del cuerpo). En este caso, se verifica que:
es cualquier matriz con derminante uno (el elemento neutro respecto al producto del cuerpo). En este caso, se verifica que:
 y que
y que 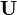 es cualquier matriz con derminante uno (el elemento neutro respecto al producto del cuerpo). En este caso, se verifica que:
es cualquier matriz con derminante uno (el elemento neutro respecto al producto del cuerpo). En este caso, se verifica que:
Una aplicación lineal entre dos espacios vectoriales de dimensión finita se puede representar mediante una matriz. La matriz asociada a la composición de aplicaciones lineales entre espacios de dimensión finita se puede calcular mediante el producto de matrices. Dadas dos aplicaciones lineales 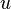 y
y  , se cumple lo siguiente:
, se cumple lo siguiente:
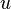 y
y  , se cumple lo siguiente:
, se cumple lo siguiente:Bibliografía:
Kline, M.
(s.f.). Determinante (matemática). Recuperado el 28 de 11 de 2015, de
Wikipedia:
https://es.wikipedia.org/wiki/Determinante_(matem%C3%A1tica)#Bibliograf.C3.ADa


No hay comentarios:
Publicar un comentario